آموزش تحلیل واریانس یک راهه (ANOVA) در SPSS
کامل‌ترین بسته آموزش SPSS را از اینجا دریافت کنید.
تحلیل واریانس یک راهه (ANOVA) یکی از تحلیل‌های پرکاربرد است که در تمامی علوم کاربرد دارد. به زبان ساده می‌توان چنین گفت که اگر شما دو یا بیش از دو گروه داشته باشید و بخواهید نمره یک متغیر را در این گروهها مقایسه کنید باید از این آزمون استفاده کنید. فرض کنید که نمره سن سه گروه کارشناسی، کارشناسی ارشد و دکتری را در دست داریم و می‌خواهیم ببینیم که آیا تفاوتی در سن این سه گروه وجود دارد یا خیر. در این صورت از تحلیل واریانس یک راهه (ANOVA) استفاده میکنیم. اگر دو گروه داشته باشیم هم می‌توانیم از تحلیل واریانس یک راهه استفاده کنیم و هم تحلیل t مستقل. با سایت دانلود پرسشنامه ایران تحقیق همراه باشید تا درباره این تحلیل بیشتر بدانید.
پیشفرض‌های تحلیل واریانس یک راهه (ANOVA)
۱- متغیر وابسته شما (در اینجا سن) باید در سطح فاصله‌ای یا نسبی باشد.
۲- متغیر مستقل (در اینجا گروه دانشگاهی) باید اسمی یا رتبه‌ای باشد.
۳- توزیع داده‌های متغیر وابسته باید به صورت نرمال باشد (تحلیل کولموگروف – اسمیرنوف).
اجرای آموزش تحلیل واریانس یک راهه (ANOVA) در SPSS
نرم افزار SPSS را باز کرده و به مسیر زیر بروید: Analyze> Compare Means> One Way Anova.
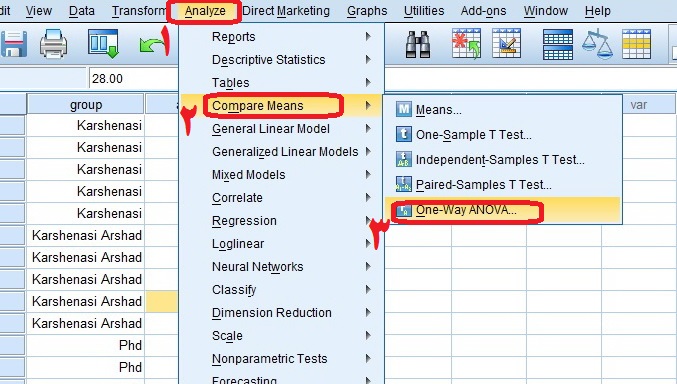
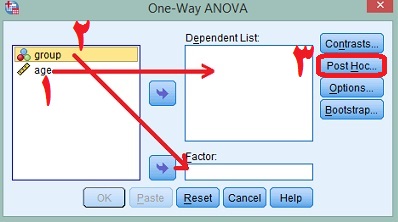
پس از باز شدن صفحه جدید، مطابق شکل زیر متغیر وابسته (سن) را در کادر Dependent List وارد کنید و در کادر Factor متغیر گروه را وارد کنید. در مرحله بعد گزینه Post Hoc را بزنید.
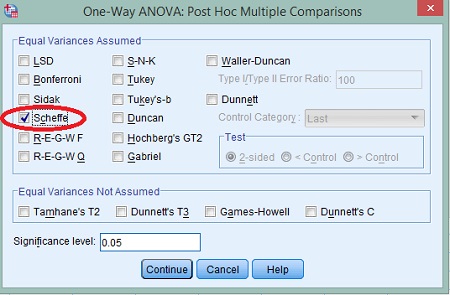
در صفحه جدید تیک گزینه Scheffe را بزنید تا تحلیل تعقیبی شفه انتخاب شود سپس بر روی گزینه Continue کلیک کنیدو پس از آن Ok را کلیک کنید. دلیل انتخاب این گزینه به سبب وجود سه گروه است. تحلیل واریانس یک راهه دو جدول به شما خواهد داد. در جدول اول نشان داده می‌شود که آیا بین این سه گروه تفاوت وجود دارد یا نه. فرض کنید که تفاوت معناداری مشاهده شد، در این صورت ما نمی‌دانیم که کدام گروه با کدام گروه دیگر تفاوت دارد. آیا سن کارشناسی از کارشناسی ارشد کمتر است؟ آیا سن کارشناسی از دکتری کمتر است؟ آیا سن کارشناسی ارشد از دکتری کمتر است؟ در واقع جدول اول پاسخ این سوالات را به شما نمی‌دهد و فقط بیان می‌کند که تفاوت وجود دارد. اما تحلیل تعقیبی شفه نشان می‌دهد که تفاوت مشاهده شده بین کدام گروه است.
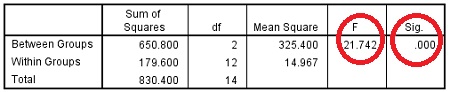
در مرحله بعد نتایج خروجی SPSS مشاهده می‌گردد. در این جدول دو شاخص F و Sig مهم هستند. اگر Sig کمتر از ۵ صدم باشد به معنی این است که بین گروهها تفاوت معناداری وجود دارد که در جدول زیر نیز این تفاوت دیده می‌شود.
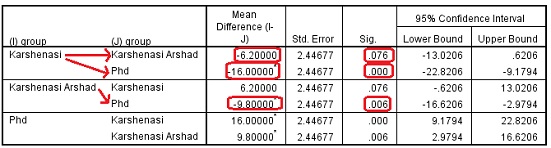
در جدول شماره بعدی نتایج تحلیل تعقیبی مشاهده می‌شود.در این جدول نتایج سه گروه به تفکیک آمده است. برای مثال در سطر اول مشاهده می‌شود که دانشجویان کارشناسی ۶ نمره از دانشجویان کارشناسی ارشد سن پایین‌تری دارند اما این تفاوت معنادار نیست درحالی که میان سن کارشناسی و دکتری و کارشناسی ارشد و دکتری تفاوت معناداری وجود دارد.
گزارش تحلیل واریانس یک راهه (ANOVA) درمقاله یا پایان نامه
یکی از سختی‌هایی که اکثر دانشجویان با آن مواجه هستند، نحوه گزارش خروجی SPSS در پایان نامه یا مقاله است. برای این کار نتایج این خروجی در جداول مربوطه آماده دانلود شده است که می‌توانید از لینک زیر دانلود کنید.
لینک دانلود نحوه گزارش نتایج تحلیل واریانس
More from my site
کنترل کننده های مرتبه کسری: روش هایی برای سنتز و کاربرد آن ها
آزمون t مستقل (آموزش SPSS: جلسه چهارم)
روش بهینه سازی بعد متغیر برای حل مسأله در مدار قرار گرفتن نیروگاه ها
کتاب لاتین حسابداری پذیرش اجتماعی (۲۰۱۵)
کتاب لاتین دوستی و شادکامی در طول زندگی و در فرهنگ ها (۲۰۱۵)
اندازه گیری وابسته به بررسی رضایت مشتری در سرویس موبایل: دیدگاه VIKOR و بررسی عاطفی
با تشکر از مطالب مفیدتون
خیلی ممنونم از مطالب مفیدی که داخل وبلاگ قرار دادید
سلام و وقت بخیر
خیلی اطلاعات مفیدی ارائه شده بود که کاربردی بودند. تشکر از زحمات شما
با سلام . بسیار عالی بود ممنونم
بسیار عالی سپاسگزارم
با سلام و تشکر از سایت خوبتون
توی کادر dependent باید متغیر وابسته رو بذاریم فکر میکنم اشتباها نوشتید متغیر مستقل
دوم اینکه سوالی که ازتون داشتم اینه که اگر در قسمت post hoc گزینه ی tukey را علامت بزنیم چه جوری خروجیش و باید تحلیل کنیم
با تشکر از شما
تشکر از شما. بله وابسته است.
در مورد آزمون توکی خروجی جدول و تمامی توضیحات دقیقا مشابه آزمون شفه است.
با سلام و احترام.
اگه در آزمون توکی بخواهیم اندازه تاثیر متغیرهای مستقل بر وابسته را ببینیم چگونه از جدول خروجی توکی نتیجه گیری کنیم و یا به عبارتی بخواهیم میزان تاثیر بین چند متغیر مستقل بر متغیر وابسته را رتبه بندی کنیم.
با تشکر
با سلام
آزمون توکی فقط به شما می گوید که آیا بین نمرات چند گروه تفاوت وجود دارد یا خیر و اگر وجود دارد معنی دار است یا خیر. برای مشاهده اندازه اثر باید از آزمون واریانس یا کوواریانس چند متغیره استفاده نمایید.
با سلام.
آزمون واریانس چند متغیره همون مانوا است؟
از کدام جدول نتایج باید بررسی شود؟
با تشکر…
بله همان مانوا است. میزان f و معناداری مهم است. اگر معناری زیر ۰٫۰۵ بود یعنی معنادار است.
تشکر از مثال و توضیحات خوبی که ارائه کردید.
سلام
سپاس از مطالب مفیدتون
ببخشید ی سوال داشتم
جدول دوم رو چطوری باید اورد اخه من گزینه ی scheffe رو میزنم ولی جدول دوم واسم نمیاد
سلام.من همه ی این تضیحات را که گفتین انجام دادم ولی فقط جدول اولی میاد.جدول دم را چطور میشه بگیرم؟ممکن داده های جدول ۲ رو هم توضیح بدین.ممنون ازتن
ببخشین راجع بع تحقیق کمی و کیفی با مثال توضیح می دین؟بعضی وقتا هم تحقیقا کمی و هم کیفی هست چه طور میشه از هم تمیزشون داد
خییییییلی ممنون واسه توضیحات
سلام. در قسمت هوک از کجا بفهمیم واریانس گروه ها برابره یا نه
با سلام و احترام
ببخشید دوتا سوال از حضورتون داشتم
برای اینکه تأثیر یک متغیر مستقل رو روی متغیر مستقل دیگه ای بسنجیم از کدام آزمون استفاده میکنیم؟
و برای بررسی تأثیر یک متغیر مستقل روی متغیر وابسته از کدام آزمون استفاده میکنیم؟
من از آزمون پیرسون و همبستگی و رگرسیون استفاده کرده بودم که گویا اشتباه بوده و اینا رابطه بین متغیرها رو بررسی میکنن
خیلی ممنون
با سلام وقتی صحبت از اثربخشی میکیند یعنی از طرح تحقیقی آزمایشی استفاده نموده اید که در این صورت از آزمونهای t، تحلیل واریانس و کواریانس می توانید استفاده کنید
اگر موضوع شما بررسی رابطه دو متغیر است که باید از آزمونهای همبستگی رگرسیون یا پیرسون استفاده کنید.
واقعیت شما نمی توانید تاثیر یک متغیر مستقل را بر روی متغیر مستقل دیگر بسنجید. یعنی تعریف شما از متغیر مستقل اشتباه است. شما می توانید اثربخشی یک متغیر مستقل بر روی یک متغیر وابسته را بسنجید.
برای توضیحات بیشتر می توانید عنوان پژوهشتان را بیان نمایید تا توضیحات دقیقتری برای شما ارایه شود.
با تشکر از مطالب مفیدتون
من سه تا داده دارم می خوام نرمالیتی بگیرم خطا میده می نویسه حداقل داده هایت باید ۵ تا باشه.چه کار کنم؟؟؟؟
سلام، دادهاتون رو باید افزایش بدید.
سلام.
امکان افزایش داده ها نباشه چکار کنیم؟
ممنون از اطلاعات مفیدتون
اگه سه نمره پیش آزمون و پس آزمون و اختلاف نمره پیش آزمون و پس آزمون رو داشتم واسه ANOVA کدوم نمره رو باید وارد کنم ؟
با سلام
برای انجام تحلیل آنوا شما می بایست تفاضل پیش آزمون و پس آزمون را وارد نمایید.
با سلام
ممنون از مطالب مفیدتون
اگر دو گروه مستقل و یک متغییر وابسته داشته باشیم و از انالیز واریانس یک طرفه استفاده کنیم تو خروجی post hoc پیام میده که باید بیشتر از دو گروه داشته باشیم ، برای مقایسه میانگین ها باید چه انالیزی انجام بدیم؟
برای آنالیز یک طرفه اگر دو گروه داشته باشید آزمون تعقیبی لازم نیست. آزمون تعقیبی برای سه گروه و بالاتر کاربرد دارد. در اینجا وقتی نتیجه آنالیز واریانس یک سویه معنی دار شد بدین معنی است که دو گروه با یکدیگر تفاوت دارند. اما وقتی سه گروه و یا بیشتر باشد به آزمون تعقیبی نیاز است چرا که باید مشخص شود تفاوت در کدام گروهها به وجود آمده است.
از مطالب ارزشمندتون بسیار ممنونم
آیا میکس آنوا و رپیتد ماژور را هم آموزش دادین من نمی تونم پیدا کنم
بسیار عالی درس دادین
درود بر شما.
سوالی داشتم در خصوص آنالیز واریانس داخل گروهی در SPSS. به عنوان مثال دو اثر تیمار و سال را داریم با روش GLM این دو اثر را به عنوان اثرات ثابت و متغیر وابسته را نیز وارد کرده و آنالیز را انجام میدهیم. حال سوال اینجاست بعضی مواقع می خواهیم داخل هر تیمار نیز برای گروههای اثر دوم آنالیز واریانس انجام دهیم در SAS این کار با استفاده از دستور BY انجام می شود
در SPSS با چه دستوری آنالیز واریانس داخل گروهی را می توان انجام داد.
با تشکر از محبت شما برای ارسال پاسخ
سلام و سپاس بابت توضیحات کاملتون.
چند سوال داشتم:
۱- برای بررسی ارتباط رفتارهای …(با ۱۲ سوال لیکرت) و میزان تحصیلات (ابتدایی، راهنمایی، دیپلم و …) و همچنین وضعیت اقتصادی (بد. متوسط. خوب) و یا تجرد و تاهل میشه از آنووا استفاده کرد؟ ۲- باید جدا هر کدام را بسنجیم؟
۳- اگه بخواهیم تاثیر همه موارد بالا را یکجا و با هم روی رفتار بسنجیم باید رگرسیون بریم؟
سپاس از لطف بی نهایتتون
سلام
بله از طریق آنووا می توانید رفتارهای … بین گروه های مختلف بررسی کنید. وقتی می گویید ارتباط بهتر است از همبستگی یا رگرسیون استفاده کنید.